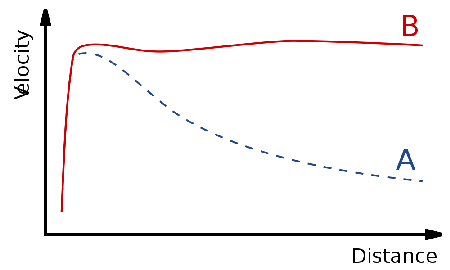
A graph of orbital speed (vertical axis) of stars in a spiral galaxy versus the distance from the centre of the galaxy (horizontal axis). Naive theory predicts that stars move slower the further out they are (curve A). But what is actually observed in real galaxies is that the speed is the same no matter how far from the centre you are (curve B).
Some of the best evidence for dark matter comes from the rotation of spiral galaxies.
In our solar system, the further out a planet is from the Sun, the slower it goes in its orbit. For example Uranus moves more than four times slower than Earth. This is exactly what our theory of gravity predicts.[1]
In a typical spiral galaxy, the stars in the spiral arms rotate around the galactic centre. It was expected that the stars further from the centre would move slower than those closer in. However in all the galaxies that we've measured, the speed of the stars doesn't change as you move out from the galactic centre.[2]
The simplest way to explain this is if there is invisible matter which exerts an extra gravitational pull on the visible matter so that it moves faster. Unlike the visible matter which is concentrated in the galactic centre, this dark matter is spread throughout the galaxy and beyond[3]. It only seems to interact with the visible matter through gravity, hence the name "dark matter". In fact the dark matter dominates visible matter in a ratio of ten to one.
Wikipedia: Dark Matter: Galaxy rotation curves
Wikipedia: Galaxy rotation problem
Theory predicts that the orbital velocity is proportional to the inverse square root of the radius (v = (GM/r)^(1/2) where M is the mass of the Sun).
Some example orbital speeds of the planets: Mercury 48 km/s, Earth 30 km/s, Uranus 7 km/s.
Using this formula we can weigh the Sun's mass M if we know the gravitational constant G.
The velocity curves of galaxies were first measured accurately in the 1960s and 1970s by Vera Rubin and her colleagues. They measured the velocities of stars in different parts of the galaxies by seeing how the light from them was blue- or redshifted compared to the average, using a spectrograph. The blue- and redshifting of light by moving bodies is analogous to the Doppler effect for sound waves.
In 1975 she and colleague Kent Ford presented their ground-breaking observation that nearly all the stars move at the same speed, regardless of distance from the galactic centre.
This implies that the mass density of the galaxies is uniform right out to the edge of the galaxy, which contradicts what we see, since the distribution of stars tapers out from the centre.
Using the rotation curve we can weigh the galaxy and find its mass. If we compare it to the total visible mass, found by adding up all the stars we see, we find that the dark matter dominates by 10:1.
Rotation of the Andromeda Nebula from a Spectroscopic Survey of Emission Regions
Profile of Vera Rubin from American Museum of Natural History
By measuring the orbital speeds of sporadic stars and hydrogen clouds outside the main galaxy, it is clear that the dark matter extends far beyond the visible galaxy in a halo.
Author: Tom Brown
Copyright: public domain
Date last modified: 13th Oct 2011
Peer-review status: Not yet peer-reviewed
http://en.wikipedia.org/wiki/File:GalacticRotation2.svg